I love learning about new computational techniques . These are my current favorite approaches.
Multilevel Bayesian Model
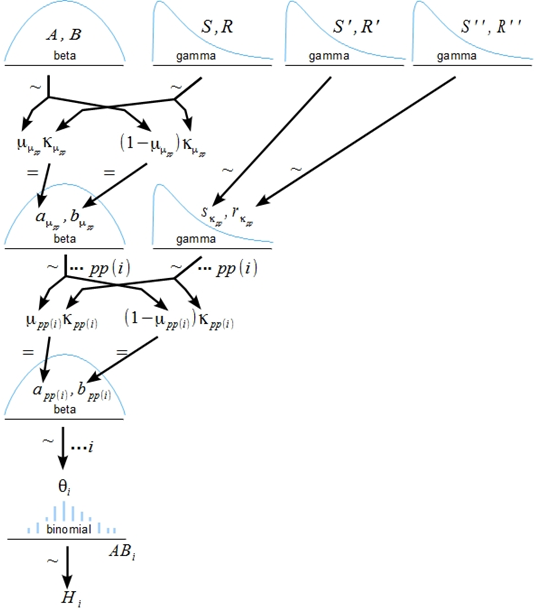
Bayesian multilevel models provide a natural and flexible way to describe the intricate relationships between predictor variables and quantify the uncertainty in estimating the effect size. I have used the R package brms (and RSTAN or finer control) for conducting bayesian analysis, which offers an incredibly rich set of functionalities. I thoroughly enjoyed playing around with different options of model specification to reflect more accurately data structure and to express more precisely theoretical assumptions. The examples include tweaking the covariance structure of the group-level effect terms, applying non-linear effects to some predictors, and customizing the underlying distribution for the response variables. This experience has made me more aware of where conventional statistical methods fall short, and piqued my interest in more sophisticated statistical techniques.
Multidimensional Scaling

Formally, Multidimensional Scaling (MDS) refers to a set of statistical techniques that take as input some measures of similarity among a group of items, and outputs a multidimensional map that represents, spatially, the similarity relationships between among items. By subjectively examining the configuration of the items in the MDS space, psychologists may infer the underlying dimensions and give psychological interpretations to them. For example, the figure to the left shows the MDS solution derived from the similarity judgments for various rock images. As you may have noticed, higher value on dimension 1 (right side) indicates lighter color and higher value on dimension 2 (upper side) indicates larger grain size. In particular, my favorite MDS technique is non-metric MDS, which, by treating the similarity measure as an ordinal variable, is robust against the non-metric properties of human-rated similarity judgments (e.g. the drop in similarity from the rating 5 to 4 on a 5-point scale may be perceived to be more pronounced than the drop from the rating 2 to 1) and against missing values in pairwise judgements. I primarily use R for conducting various dimensionality reduction analyses and visualizing the results.
Generalized Context Model
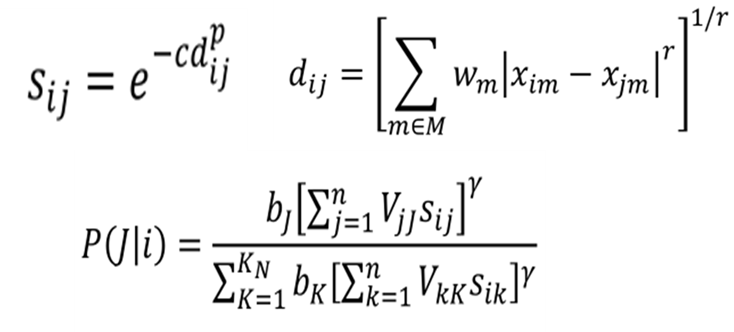
Generalized context model (GCM) is a computational model that describes the cognitive process involved in category learning. Essentially, it postulates that people categorize a novel object by comparing how similar it is to all examples in each of the alternative learned categories. Moreover, The model provides a framework into which various mechanisms can be incorporated to explain factors such as how similarity is judged in relation to multiple perceptual features, how category sparsity influence the similarity judgement, and how strong people’s tendencies are to select the category with the maximum similarity, to name a few. This approach has enabled us to investigate a wide range of theoretical issues in category learning. Given that classification and conceptualization play such a crucial role in almost all academic courses, I believe that GCM will have promising applications beyond the laboratory.
Multimodal Neural Network
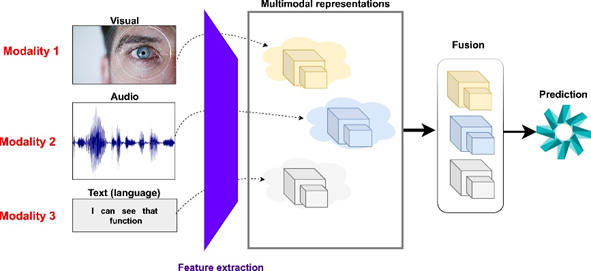
…
